OpenCV 学习笔记（4）

图像复原。

函数说明

Mat 构造函数

1	Mat dstImage = Mat(srcImage.size(), srcImage.type());

Mat 值拷贝

1 2	Mat dstImage; srcImage.copyTo(dstImage);

Mat 截取

Mat imageROI;
imageROI = image(const Rect& roi);
imageROI = image(Range rowRange, Range colRange);
imageROI = image(const Range* ranges);
roi = Rect(x, y, width, height);
roi = Rect(point1, point2);
rowRange = Range(startrow, endrow);
rowRange = Range::all();	// select all the rows

ranges - 每个维度选取的范围构成的数组

Sum / Mean

返回数组元素的和，对于每个通道独立。

1 2	Scalar sum(InputArray src); Scalar mean(InputArray src);

divide

两个数组间元素的除法。

1 2	void divide(InputArray src1, InputArray src2, OutputArray dst, double scale=1, int dtype=-1)

参数说明

src1 - 第一个输入数组
src2 - 第二个输入数组
dst - 输出数组，与输入数组具有相同的大小和类型
scale - 可选的比例参数
- $dst = (scale \cdot src1) / src2$
dtype - 可选的输出数组深度；若为-1，则输出数组深度为 src2.depth() ，但为了防止数组除法（array-by-array division）的情况，当 src1.depth()==src2.depth 时，只能设定-1.

函数说明

当 src2(I) 为0时，dst(I) 也为0
多通道数组的各不同通道独立计算

问题描述

复原椒盐噪声图像

原图像如下图所示。向其中加入椒盐噪声，并采用

算术均值滤波
几何均值滤波
谐波均值滤波
中值滤波

过滤噪声，复原图像。

点此下载

复原运动模糊图像

运动模糊图像如下图所示。采用维纳滤波进行图像复原。

点此下载

程序实现

加入椒盐噪声

设加入噪声的比例为p。在每个像素位置，生成 [0,1) 的随机数，当随机数值小于0.5p时，加入胡椒噪声；当随机数值在 [0.5p, p) 范围内时，加入盐噪声。

//加入椒盐噪声
Mat addNoise(const Mat &srcImage, double p) {
    Mat dstImage;
    srcImage.copyTo(dstImage);
    for (int i = 0; i < dstImage.rows; i++) {
        for (int j = 0; j < dstImage.cols; j++) {
            //生成 [0,1) 的随机数
            double randnum;
            randnum = rand() / double(RAND_MAX);
            //加入胡椒噪声
            if (randnum < 0.5 * p) dstImage.at<Vec3b>(i, j) = { 0, 0, 0 };
            //加入盐噪声
            else if (randnum < p) dstImage.at<Vec3b>(i, j) = { 255, 255, 255 };
        }
    }
    return dstImage;
}

加入椒盐噪声后的图像：

边界扩展

为了便于边界点的模板操作，对原图的边界进行扩展。目标图像上的像素坐标在扩展图像上对应于窗口区域的左上角位置。补0扩展在滤波操作中会显著减小边界点的灰度值，这里采用反射扩展。

Mat expImage, dstImage, imageROI;
srcImage.copyTo(expImage);
int a, b;
a = (ksize.width - 1) / 2;
b = (ksize.height - 1) / 2;
//边界反射扩展，目标图像上的像素坐标对应于窗口区域的左上角位置
copyMakeBorder(expImage, expImage, b, b, a, a, BORDER_REFLECT);
dstImage = Mat(srcImage.size(), srcImage.type());

椒盐噪声滤波

算术均值滤波

令$S_{xy}$表示中心在$(x,y)$，尺寸为$m\times n$的矩形子图像窗口的坐标集。算术均值滤波可表示为：
$$\hat f(x,y)=\frac{1}{mn}\sum_{(s,t)\in S_{xy}}{g(x,y)}$$

for (int i = 0; i < dstImage.rows; i++) {
    for (int j = 0; j < dstImage.cols; j++) {
        imageROI = expImage(Rect(j, i, ksize.width, ksize.height));
        //计算算数均值
        Vec4b m = (Vec4b)mean(imageROI);
        dstImage.at<Vec3b>(i, j) = { m[0], m[1], m[2] };
    }
}

几何均值滤波

每个被复原像素由子图像窗口中像素点的乘积结果求$\frac{1}{mn}$次幂得到：
$$\hat f(x,y)=\left(\prod_{(s,t)\in S_{xy}}{g(x,y)} \right) ^{\frac{1}{mn}}$$

for (int i = 0; i < dstImage.rows; i++) {
    for (int j = 0; j < dstImage.cols; j++) {
        //初始化乘积
        Vec3d product = { 1, 1, 1 };
        for (int m = 0; m < ksize.height; m++) {
            for (int n = 0; n < ksize.width; n++) {
                //累乘像素灰度值
                product[0] *= expImage.at<Vec3b>(i + m, j + n)[0];
                product[1] *= expImage.at<Vec3b>(i + m, j + n)[1];
                product[2] *= expImage.at<Vec3b>(i + m, j + n)[2];
            }
        }
        //计算几何均值
        Vec3b c;
        double b = 1.0 / (ksize.width * ksize.height);
        c[0] = (uchar)pow(product[0], b);
        c[1] = (uchar)pow(product[1], b);
        c[2] = (uchar)pow(product[2], b);
        dstImage.at<Vec3b>(i, j) = c;
    }
}

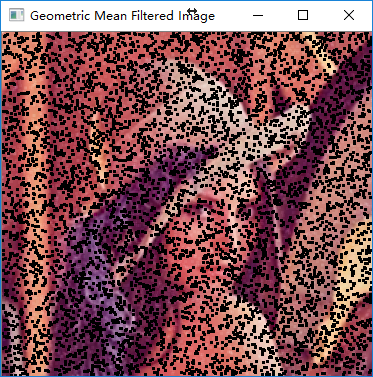
可以看出，几何均值滤波不能过滤胡椒噪声，反而会扩大胡椒噪声。由几何均值滤波公式，当窗口区域中有像素点的灰度值为0时，计算得到的几何均值就为0。即几何均值滤波后，胡椒噪声周围的像素点都将变为黑点。
考虑到几何均值滤波可以过滤盐噪声，可对图像中的胡椒噪声取反，变为盐噪声，再进行滤波。

加入一行代码：

1	if (expImage.at<Vec3b>(i + m, j + n)[0] == 0)expImage.at<Vec3b>(i + m, j + n) = {255, 255, 255};

对胡椒噪声取反后，几何均值滤波得到的图像：

谐波均值滤波

谐波均值滤波可表示为：
$$\hat f(x,y)=\frac{mn}{\sum \limits_{(s,t)\in S_{xy}}{\frac{1}{g(x,y)}}}$$

for (int i = 0; i < dstImage.rows; i++) {
    for (int j = 0; j < dstImage.cols; j++) {
        //初始化分母（灰度值倒数之和）
        Vec3d den = { 0, 0, 0 };
        for (int m = 0; m < ksize.height; m++) {
            for (int n = 0; n < ksize.width; n++) {
                //累加灰度值倒数
                den[0] += 1.0 / expImage.at<Vec3b>(i + m, j + n)[0];
                den[1] += 1.0 / expImage.at<Vec3b>(i + m, j + n)[1];
                den[2] += 1.0 / expImage.at<Vec3b>(i + m, j + n)[2];
            }
        }
        //计算谐波均值
        Vec3b c;
        c[0] = (uchar)(ksize.width * ksize.height / den[0]);
        c[1] = (uchar)(ksize.width * ksize.height / den[1]);
        c[2] = (uchar)(ksize.width * ksize.height / den[2]);
        dstImage.at<Vec3b>(i, j) = c;
    }
}

同几何均值滤波类似，谐波均值滤波也不能过滤胡椒噪声。由谐波均值滤波公式，当窗口区域中有像素点的灰度值为0时，分母为无穷大，计算得到的谐波均值为0。即谐波均值滤波后，胡椒噪声周围的像素点都将变为黑点。
同样的，对图像中的胡椒噪声取反，变为盐噪声，再进行滤波。滤波得到的图像：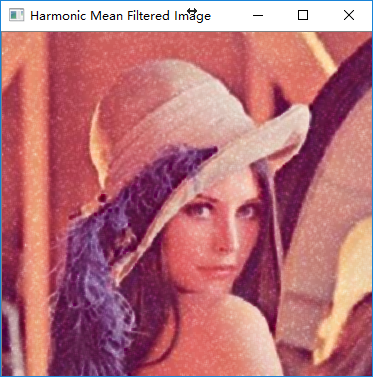

中值滤波

取子图像窗口中像素点灰度的中值作为被复原像素点的灰度值：
$$\hat f(x,y)=\mathop{medium}\limits_{(s,t)\in S_{xy}}{g(x,y)}$$

首先考虑通过对窗口区域像素的灰度值进行排序来计算中值。对于大小为 $n\times n$ 的模板核，冒泡排序的时间复杂度为$O(n^4)$，快速排序的时间复杂度为$O(n^2\log n)$。显然对于较大的模板核，计算时间很长。

论文《AFast Two-Dimensional Median Filtering Algorithm》[1] 中提出了一种时间复杂度为$O(n)$的中值计算方法。

利用灰度直方图计算中值
利用窗口区域的灰度直方图计算其像素点中值，对于深度一定的图像，计算时间为常数，即复杂度为$O(1)$。

//在直方图中计算中值
int calcMedium(const Mat &hist, int total) {
    //计算中值时，停止计数值为像素总数的 1/2
    int stopCount = total / 2;
    float s = 0;
    for (int i = 0; i < hist.size[0]; i++) {
        s += hist.at<float>(i);
        if (s > stopCount) return i;
    }
}

计算灰度直方图
在每一行的起始，计算窗口区域的灰度直方图，在从一个像素点移动到与之相邻（水平或垂直方向）的像素点时，动态地更新灰度直方图。如下图所示。对于 $n\times n$ 的窗口区域，每次移动在直方图中执行n次减法与n次加法，时间复杂度为$O(n)$。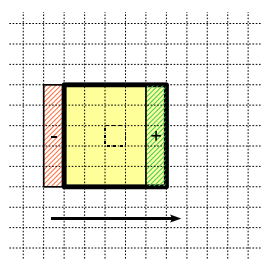

[2]

for (int i = 0; i < dstImage.rows; i++) {
    imageROI = expImage(Rect(0, i, ksize.width, ksize.height));
    //将三通道的ROI分割为三个单通道图像
    Mat ROIplane[3];
    split(imageROI, ROIplane);
    //计算每个单通道图像的直方图
    Mat hist[3];
    int channel = 0;
    int histSize = 256;
    int dims = 1;
    float hranges[] = { 0, 255 };
    const float *ranges[] = { hranges };
    calcHist(&ROIplane[0], 1, &channel, Mat(), hist[0], dims, &histSize, ranges);
    calcHist(&ROIplane[1], 1, &channel, Mat(), hist[1], dims, &histSize, ranges);	
    calcHist(&ROIplane[2], 1, &channel, Mat(), hist[2], dims, &histSize, ranges);
    for (int j = 0; j < dstImage.cols; j++) {
        if (j > 0) {
            //更新直方图，删去原ROI最左边的列，添加右边一列
            for (int k = 0; k < ksize.height; k++) {
                hist[0].at<float>(expImage.at<Vec3b>(i + k, j - 1)[0]) -= 1;
                hist[0].at<float>(expImage.at<Vec3b>(i + k, j + ksize.width - 1)[0]) += 1;
                hist[1].at<float>(expImage.at<Vec3b>(i + k, j - 1)[1]) -= 1;
                hist[1].at<float>(expImage.at<Vec3b>(i + k, j + ksize.width - 1)[1]) += 1;
                hist[2].at<float>(expImage.at<Vec3b>(i + k, j - 1)[2]) -= 1;
                hist[2].at<float>(expImage.at<Vec3b>(i + k, j + ksize.width - 1)[2]) += 1;
            }
        }
        //计算中值
        Vec3b m;
        int total = ksize.width * ksize.height;
        m[0] = calcMedium(hist[0], total);
        m[1] = calcMedium(hist[1], total);
        m[2] = calcMedium(hist[2], total);
        dstImage.at<Vec3b>(i, j) = m;
    }
}

运动模糊图像复原

运动模糊的退化函数

假设图像以一定的速率做匀速直线运动，x, y 方向上的速度分别为 $x_0(t)=\frac{at}{T}$，$y_0(t)=\frac{bt}{T}$ 。运动模糊的退化函数可表示为
$$H(u,v)=\frac{T}{\pi (ua+vb)}\sin\left[\pi (ua+vb)\right]e^{-j\pi (ua+vb)}=\frac{T}{\pi (ua+vb)}\sin\left[\pi (ua+vb)\right](\cos\left[\pi (ua+vb)\right]-j\sin\left[\pi (ua+vb)\right])=T\frac{\sin\left[2\pi (ua+vb)\right]}{2\pi (ua+vb)}+jT\frac{\cos\left[2\pi (ua+vb)\right]-1}{2\pi (ua+vb)}$$

// 运动模糊
Mat motionBlur(Size msize, double a, double b, double T) {
    //建立一个2通道32位浮点数的矩阵，通道1存放实部，通道2存放虚部
    Mat degMat = Mat(msize, CV_32FC2);
    double k;
    for (int i = 0; i < msize.width; i++) {
        for (int j = 0; j < msize.height; j++) {
            k = 2 * PI * (i * a + j * b);
            //处理分母为0的情况
            if (k == 0) k = 0.0001;
            degMat.at<Vec2f>(i, j)[0] = T * sin(k) / k;
            degMat.at<Vec2f>(i, j)[1] = T * (cos(k) - 1) / k;
        }
    }
    return degMat;
}

维纳滤波

维纳滤波可近似表示为
$$\hat F(u,v)=\left[\frac{1}{H(u,v)}\frac{|H(u,v)|^2}{|H(u,v)|^2+K}\right]G(u,v)$$
其中，K 为信噪比。

设$G(u,v)=a_1+jb_1$，$H(u,v)=a_2+jb_2$。则上述公式可化为：
$$\hat F(u,v)=\frac{a_1+jb_1}{a_2+jb_2}\cdot\frac{|H(u,v)|^2}{|H(u,v)|^2+K}=\frac{(a_1+jb_1)(a_2-jb_2)}{(a_2+jb_2)(a_2-jb_2)}\cdot\frac{|H(u,v)|^2}{|H(u,v)|^2+K}=\frac{(a_1a_2+b_1b_2)+j(a_2b_1-a_1b_2)}{(a_2^2+b_2^2)+K}$$

//维纳滤波
Mat wienerFilter(const Mat &blurMat, const Mat &degMat, double K = 0.01) {
    Mat blur_plane[2], deg_plane[2], res_plane[2];
    //分割2通道的矩阵，提取实部和虚部
    split(blurMat, blur_plane);
    split(degMat, deg_plane);
    Mat mul[6];
    multiply(deg_plane[0], deg_plane[0], mul[0]);
    multiply(deg_plane[1], deg_plane[1], mul[1]);
    multiply(blur_plane[0], deg_plane[0], mul[2]);
    multiply(blur_plane[1], deg_plane[1], mul[3]);
    multiply(blur_plane[1], deg_plane[0], mul[4]);
    multiply(blur_plane[0], deg_plane[1], mul[5]);
    divide(mul[2] + mul[3], mul[0] + mul[1] + K, res_plane[0]);
    divide(mul[4] - mul[5], mul[0] + mul[1] + K, res_plane[1]);
    Mat resMat;
    merge(res_plane, 2, resMat);
    return resMat;
}

图像复原

对模糊图像进行傅里叶变换，采用变换得到的频谱与估计的退化函数进行维纳滤波，再对滤波后的频谱进行傅里叶反变换，得到复原图像。

int main() {
    //读取模糊图像
    Mat blurImage;
    blurImage = imread("blur.jpg");
    imshow("Blur Image", blurImage);
    //分割RGB三通道图像
    Mat blur_plane[3], blur_spec[3];
    split(blurImage, blur_plane);
    //离散傅里叶变换
    blur_spec[0] = performDFT(blur_plane[0]);
    blur_spec[1] = performDFT(blur_plane[1]);
    blur_spec[2] = performDFT(blur_plane[2]);
    //生成运动模糊退化函数
    Mat H;
    H = motionBlur(Size(blur_spec[0].cols, blur_spec[0].rows), 0.0005, -0.0001, 1);
    //维纳滤波，傅里叶逆变换
    Mat res_plane[3];
    res_plane[0] = performIDFT(wienerFilter(blur_spec[0], H, 0.02));
    res_plane[1] = performIDFT(wienerFilter(blur_spec[1], H, 0.02));
    res_plane[2] = performIDFT(wienerFilter(blur_spec[2], H, 0.02));
    //合成三通道图像
    Mat resImage;
    merge(res_plane, 3, resImage);
    imshow("Restored Image", resImage);
    waitKey(0);
    return 0;
}

在当前设置的退化函数参数下，去模糊的效果不明显，同时有一定的颜色失真。

Matlab 复原

Matlab 下调用函数进行图像复原：

%读取模糊图像
blur = im2double(imread('blur.jpg'));
figure(1);imshow(blur);
title('Blur Image');
%运动模糊卷积核
len = 21;
theta = 11;
h = fspecial('motion', len, theta);
%维纳滤波复原，信噪比设为0.02
res = deconvwnr(blur, h, 0.02);
figure(2);imshow(res);
title('Restored Image');

得到的复原图像：

参考文献

[1] Huang T, Yang G,Tang G. A fast two-dimensional median filtering algorithm[J]. IEEE Transactionson Acoustics, Speech, and Signal Processing, 1979, 27(1): 13-18.
[2] Perreault S, Hébert P. Medianfiltering in constant time[J]. IEEE transactions on image processing, 2007,16(9): 2389-2394.