OpenCV 学习笔记（3）

对图像进行傅里叶变换和频域滤波。

频域增强

频域增强的实现方法

将图像从图像空间转换到频域空间
计算图像的傅里叶变换： $f(x,y)$ –> $F(u,v)$
在频域空间对图像进行增强
将其与频域滤波器相乘: $G(u,v) = F(u,v) H(u,v)$
将增强后的图像再从频域空间转换到图像空间
进行傅里叶反变换: $G(u,v)$ –> $g(x,y)$

周期折叠误差改进

图像进行傅立叶变换，需将其看作周期函数的一个周期；
周期函数进行卷积，为避免周期折叠误差，需对函数进行补零扩展。$f(x,y)$、$h(x,y)$ 均补零扩充为 $P\times Q$，$P=2N-1$，$Q=2N-1$.
具体步骤如下：
1.用 $(-1)^{x+y}$ 乘以输入图像 $f(x,y)$ 来进行中心变换；
$$f(x,y)(-1)^{x+y}\Leftrightarrow F(u-\frac{M}{2},v-\frac{N}{2})$$
2.由 1. 计算图像的 DFT，得到 $F(u,v)$ ；
3.用频域滤波器 $H(u,v)$ 乘以 $F(u,v)$ ；
4.将 3. 中得到的结果进行IDFT；
5.取 4. 中结果的实部；
6.用 $(-1)^{x+y}$ 乘以 5. 中的结果，即可得滤波图像。

高频增强滤波

实现步骤

傅里叶变换：$G(u,v) = H(u,v)F(u,v)$
高频增强转移函数：$H_e(u,v) = a \cdot H(u,v) + b$
高频增强输出图的傅里叶变换：
$G_e(u,v) = a \cdot G(u,v) + b \cdot F(u,v)$
傅里叶反变换：
$g_e(x,y) = a \cdot g(x,y) + b \cdot f(x,y)$

特点

在原始图像的基础上叠加一些高频成分，因而增强图中高频成分增多。
既保留了原图的灰度层次，又锐化了边缘。

函数说明

getOptinalDFTSize

返回最佳的DFT尺寸。
在官方文档中的定义为：

1	int getOptimalDFTSize(int vecsize)

参数说明

vecsize - 向量尺寸

函数说明

当对两个数组计算卷积或对数组频域分析时，对输入图像进行补零扩展可以提高运算速度。
大小为 2 的整数次幂的数组具有最快的处理速度。
大小为 2，3，5 乘积的数组能被高效地处理。
getOptimalDFTSize 函数返回一个不小于 vecsize 的最小整数 N，$N = 2^p \cdot 3^q \cdot 5^r$。
若函数不能直接得到最佳的DFT尺寸(当前DFT仅支持偶数维大小的向量)，则可采用 getOptimalDFTSize((vecsize+1)/2)*2 。

copyMakeBorder

扩展图片边界。
在官方文档中的定义为：

1
2
3

void copyMakeBorder(InputArray src, OutputArray dst, 
        int top, int bottom, int left, int right, 
        int borderType, const Scalar& value=Scalar())

参数说明

src - 原图像
dst - 目标图像，大小为 Size(src.cols+left+right, src.rows+top+bottom)
top, bottom, left, right - 边界所需扩展的像素数
borderType - 边界类型，取值如下：
BORDER_REPLICATE | aaaaaa|abcdefgh|hhhhhhh | 重复
BORDER_REFLECT | fedcba|abcdefgh|hgfedcb | 反射
BORDER_REFLECT_101 | gfedcb|abcdefgh|gfedcba | 反射101，不反射边界值
BORDER_WRAP | cdefgh|abcdefgh|abcdefg | 包装
BORDER_CONSTANT | iiiiii|abcdefgh|iiiiiii | i 为常量
value - 当 borderType == BORDER_CONSTANT 时的边界值

merge

将多个单通道图像合成一个多通道图像。
在官方文档中的定义为：

1	void merge(const Mat* mv, size_t count, OutputArray dst)

参数说明

mv - 输入的多个单通道图像数组，所有的图像必须具有相同的尺寸和深度
count - 输入单通道图像数
dst - 输出的多通道图像

split

将多通道图像分割成多个单通道图像。
在官方文档中的定义为：

1	void split(const Mat& src, Mat* mvbegin)

参数说明

src - 输入的多通道图像
mvbegin - 输出的多个单通道图像，第1维是通道数

dft

离散傅里叶变换。
在官方文档中的定义为：

1	void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0)

参数说明

src - 输入实数或复数数组
dst - 输出数组
flags - 变换标识，默认值为0（傅里叶变换），可取以下值的组合：
- DFT_INVERSE - 1维或2维傅里叶反变换
- DFT_SCALE - 缩放结果值：将值除以数组元素数；通常和 DFT_INVERSE 组合使用。
- DFT_COMPLEX_OUTPUT - 进行傅里叶变换，输入为实数数组时，输出复共轭对称。
- DFT_REAL_OUTPUT - 进行傅里叶反变换，输入复共轭对称时，输出为实数数组。
nonzeroRows - 当这个值不为0时，认为只有输入数组的第一个nonzeroRows行（DFT_INVERSE未被设置），或输出数组的第一个nonzeroRows行（DFT_INVERSE被设置）包含非零元素。

idft

离散傅里叶反变换。
在官方文档中的定义为：

1	void idft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0)

参数说明

src - 输入的浮点数实数或复数数组
dst - 输出数组
flags - 变换标识
nonzeroRows - 需要运算的行

magnitude

计算2维向量的幅值。
在官方文档中的定义为：

1	void magnitude(InputArray x, InputArray y, OutputArray magnitude)

参数说明

x - x坐标的浮点数组
y - y坐标的浮点数组
magnitude - 输出的幅值数组

normalize

归一化数组的范数或值的范围。
在官方文档中的定义为：

void normalize(InputArray src, OutputArray dst, 
        double alpha=1, double beta=0, 
        int norm_type=NORM_L2, int dtype=-1, 
        InputArray mask=noArray())

参数说明

src - 输入数组
dst - 输出数组
alpha - 值范围归一化时的下界
beta - 值范围归一化时的上界
norm_type - 归一化类型。可取以下值：
- NORM_MINMAX - 值范围归一化
- NORM_INF - 无穷范数归一化
- NORM_L1 - 1 范数归一化
- NORM_L2 - 2 范数归一化
dtype - 如果为负，输出数组与输入数组具有相同的类型；否则，输出数组与输入具有相同的通道数，深度为 CV_MAT_DEPTH(dtype)
mask - 可选运算掩码

multiply

计算两个数组每个元素的乘积。
在官方文档中的定义为：

1 2	void multiply(InputArray src1, InputArray src2, OutputArray dst, double scale=1, int dtype=-1 )

参数说明

src1 - 第一个输入数组
src2 - 第二个输入数组
dst - 输出数组，与输入数组具有相同的大小和类型
scale - 可选的比例参数
- $dst = scale \cdot src1 \cdot src2$

程序实现

有如下原图和加噪图像，分别对两幅图进行傅里叶变换。并对加噪图像进行频域滤波。

点此下载

实现如下：

#include <opencv2\opencv.hpp>
#include <opencv2\core\core.hpp>
#include <opencv2\highgui\highgui.hpp>
using namespace cv;
using namespace std;
void centralize(Mat &image)
{
    for (int i = 0; i < image.rows; i++) {
        for (int j = 0; j < image.cols; j++) {
            image.at<float>(i, j) *= pow(-1, i + j);
        }
    }
}
Mat performDFT(const Mat &srcImage)
{
    //获得最佳的DFT尺寸
    int m, n;
    m = getOptimalDFTSize(srcImage.rows);
    n = getOptimalDFTSize(srcImage.cols);
    //边界扩展
    Mat dstImage;
    srcImage.convertTo(dstImage, CV_32F);
    copyMakeBorder(dstImage, dstImage, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));
    //中心化
    centralize(dstImage);
    //新建两页的浮点数array，其中第一页用中心化后的图像初始化，第二页初始化为0 
    Mat imgArray[] = { Mat_<float>(dstImage), Mat::zeros(dstImage.size(), CV_32F) };
    //把两页合成一个2通道的图像
    merge(imgArray, 2, dstImage);
    //dft，傅里叶变换结果为复数。通道1存的是实部，通道2存的是虚部。
    dft(dstImage, dstImage);
    return dstImage;
}
Mat calcSpectrum(const Mat &srcImage)
{
    //将二通道图像分割成两个单通道图像
    Mat imgArray[2];
    split(srcImage, imgArray);
    //计算幅值
    Mat dstImage;
    magnitude(imgArray[0], imgArray[1], dstImage);
    //取log(1+|F|)
    dstImage += Scalar(1);
    log(dstImage, dstImage);
    //归一化
    normalize(dstImage, dstImage, 0, 1, NORM_MINMAX);
    return dstImage;
}
Mat filter(const Mat &srcImage)
{
    //巴特沃斯滤波器
    Mat BF(srcImage.size(), CV_32F);
    Mat dstImage(srcImage.size(), CV_32F);
    int Dl = 1500, Dh = 40000;
    int n = 4;
    float lp, hp;
    for (int i = 0; i < srcImage.rows; i++) {
        for (int j = 0; j < srcImage.cols; j++) {
            //低通部分
            lp = 1 / (1 + pow(((pow((i + 1 - srcImage.rows / 2), 2) + pow((j + 1 - srcImage.cols / 2), 2)) / (Dl ^ 2)), n));
            //高通部分
            hp = 1 / (1 + pow((Dh ^ 2) / ((pow((i + 1 - srcImage.rows / 2), 2) + pow((j + 1 - srcImage.cols / 2), 2))), n));
            BF.at<float>(i, j) = lp + hp;
        }
    }
    //调整带阻滤波器，使阻带部分衰减至10%（而非完全阻断）
    normalize(BF, BF, 0.1, 1, CV_MINMAX);
    //频域滤波
    multiply(srcImage, BF, dstImage);
    imshow("Butterworth Filter", BF);
    return dstImage;
}
Mat performIDFT(const Mat &srcImage)
{
    //将二通道图像分割成两个单通道图像
    Mat imgArray[2];
    split(srcImage, imgArray);
    //频域滤波
    imgArray[0] = filter(imgArray[0]);
    imgArray[1] = filter(imgArray[1]);
    //把滤波后的实部和虚部合成一个2通道的图像
    Mat dstImage;
    merge(imgArray, 2, dstImage);
    //idft，取实部
    idft(dstImage, dstImage, DFT_REAL_OUTPUT);
    //中心化
    centralize(dstImage);
    //归一化
    normalize(dstImage, dstImage, 0, 1, CV_MINMAX);
    return dstImage;
}
int main()
{
    //读取原图
    Mat srcImage = imread("origin.jpg", 0);
    imshow("Source Image", srcImage);
    if (!srcImage.data)
    {
        cout << "fail to load image!" << endl;
    }
    //计算原图频谱
    Mat srcDFT, srcSpec;
    srcDFT = performDFT(srcImage);
    srcSpec = calcSpectrum(srcDFT);
    imshow("Source Spectrum Image", srcSpec);
    //读取加噪图像
    Mat noiImage = imread("addnoise.jpg", 0);
    imshow("Noisy Image", noiImage);
    if (!noiImage.data)
    {
        cout << "fail to load image!" << endl;
    }
    //计算加噪图频谱
    Mat noiDFT, noiSpec, filSpec;
    noiDFT = performDFT(noiImage);
    noiSpec = calcSpectrum(noiDFT);
    imshow("Noisy Spectrum Image", noiSpec);
    //频域滤波
    filSpec = filter(noiSpec);
    imshow("Filtered Spectrum", filSpec);
    Mat dstImage = performIDFT(noiDFT);
    //裁剪扩展的边界
    dstImage = dstImage(Rect(0, 0, noiImage.cols, noiImage.rows));
    imshow("Filtered Image", dstImage);
    waitKey(0);
    return 0;
}

运行结果

原图频谱
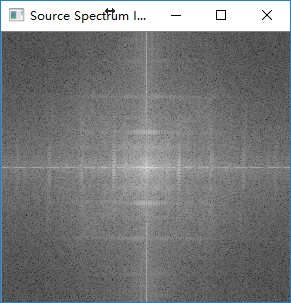
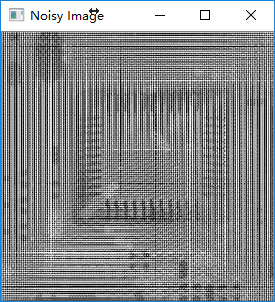
加噪图频谱
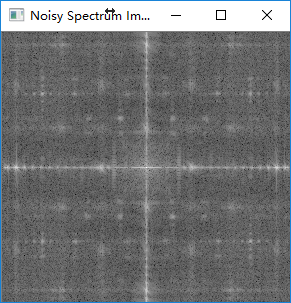
频域滤波器
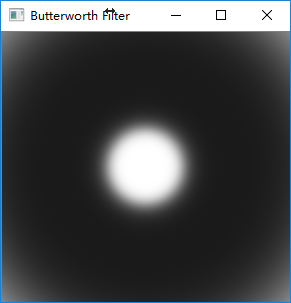
滤波后的图像

（效果不太好，我尽力了 = =||）